动态规划
完全背包问题
每种物品无限个
-
状态转移
以前一直对完全背包的状态转移方程**f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i])里面的f[i][j-v[i]]+w[i]**似懂非懂,今天看到一个比较好的解释
1.已知完全背包还有状态转移方程
f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i],f[i-1][j-2*v[i]]+2*w[i],...,f[i-1][j-k*v[i]]+k*w[i]) (j-k*v[i]>=0)
2.故可得f[i][j-v[i]] = max(f[i-1][j-v[i]],f[i-1][j-2*v[i]]+*w[i],...,f[i-1][j-k*v[i]]+(k-1)*w[i])
3.第二步的式子左右加上w[i],右边带入一式即可得**f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i])**
-
排列型背包和组合型背包
- 排列型背包外层循环价值,内层循环物品
- 组合型背包外层循环物品,内层循环价值
多重背包
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
直接拆分法
当成01背包做,效率低
二进制拆分法
将每种物品按二进制1,2,4,…,2^k^ ,s-2^k+1^+1拆分成log(si)个,降低时间复杂度
1 | k=1 |
分组背包
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i是组号,j是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
做法
直接三重循环,最内层循环更新第i组每个物品对应的 最优解
1 | for (int i = 1; i <= n; i++ ){ |
背包问题输出方案
本质是最短路问题
1 |
|
区间DP
方法:
1.循环
外层枚举区间长度,内层枚举左端点位置,对[l,r]区间内的序列进行dp
1 | for (int len = 1; len <= n; len++) { |
2.记忆化搜索
模型:
1.环形问题
将环变成链,即在原本的链之后再拼接上一条链,对新的链进行dp
状态机DP
dp数组多加一维表示当前的状态,有点类似状态压缩dp,每次dp进行状态之间的转移(根据前一次的状态)
状态压缩DP
棋盘类状压DP:用01二进制表示状态,先预处理合法的状态(减少时间复杂度),再根据合法状态的合法转移进行dp
树形DP
第一维通常是节点编号,多数时候用递归实现树形DP,对于每个节点x,先递归在它的每个子节点上进行DP,回溯时从子节点向节点x进行状态转移
数位DP
技巧
1.[x,y]转化为[1,y] - [1,x-1]
2.用树的思想,考虑每一位的情况**(注意树的最右边的情况需要特判一下)**
例题:计数问题
给定两个整数 a 和 b,求 a 和 b 之间的所有数字中0~9的出现次数。
例如,a=1024,b=1032,则 a 和 b 之间共有9个数如下:
1024 1025 1026 1027 1028 1029 1030 1031 1032
其中‘0’出现10次,‘1’出现10次,‘2’出现7次,‘3’出现3次等等…
思路
把整个数拆成每一位,从最高位向最低位看。设当前这一位为x,则当前位分成[0,x)和x两种情况。第一种情况直接处理,剩下的就是当前位为x的情况,继续看后面的数位,重复这个操作。直到最后一位时,剩下的就是原数,判断是否符合条件即可。
技巧
再求区间[a,b]中满足性质的数时,可以转化为求[1,b]的答案减[1,a - 1]的答案
例题:数字游戏
由于科协里最近真的很流行数字游戏。
某人又命名了一种取模数,这种数字必须满足各位数字之和 mod N 为 0。
现在大家又要玩游戏了,指定一个整数闭区间 [a.b],问这个区间内有多少个取模数。
输入格式
输入包含多组测试数据,每组数据占一行。
每组数据包含三个整数 a,b,N。
输出格式
对于每个测试数据输出一行结果,表示区间内各位数字和 mod N 为 0 的数的个数。
数据范围
1≤a,b≤231−1,
1≤N<100
输入样例:
1 | 1 19 9 |
输出样例:
1 | 2 |
1 |
|
计数DP
不重不漏,避免子问题重叠,通常要预处理
闫氏DP分析法
from:https://www.acwing.com/file_system/file/content/whole/index/content/406072/
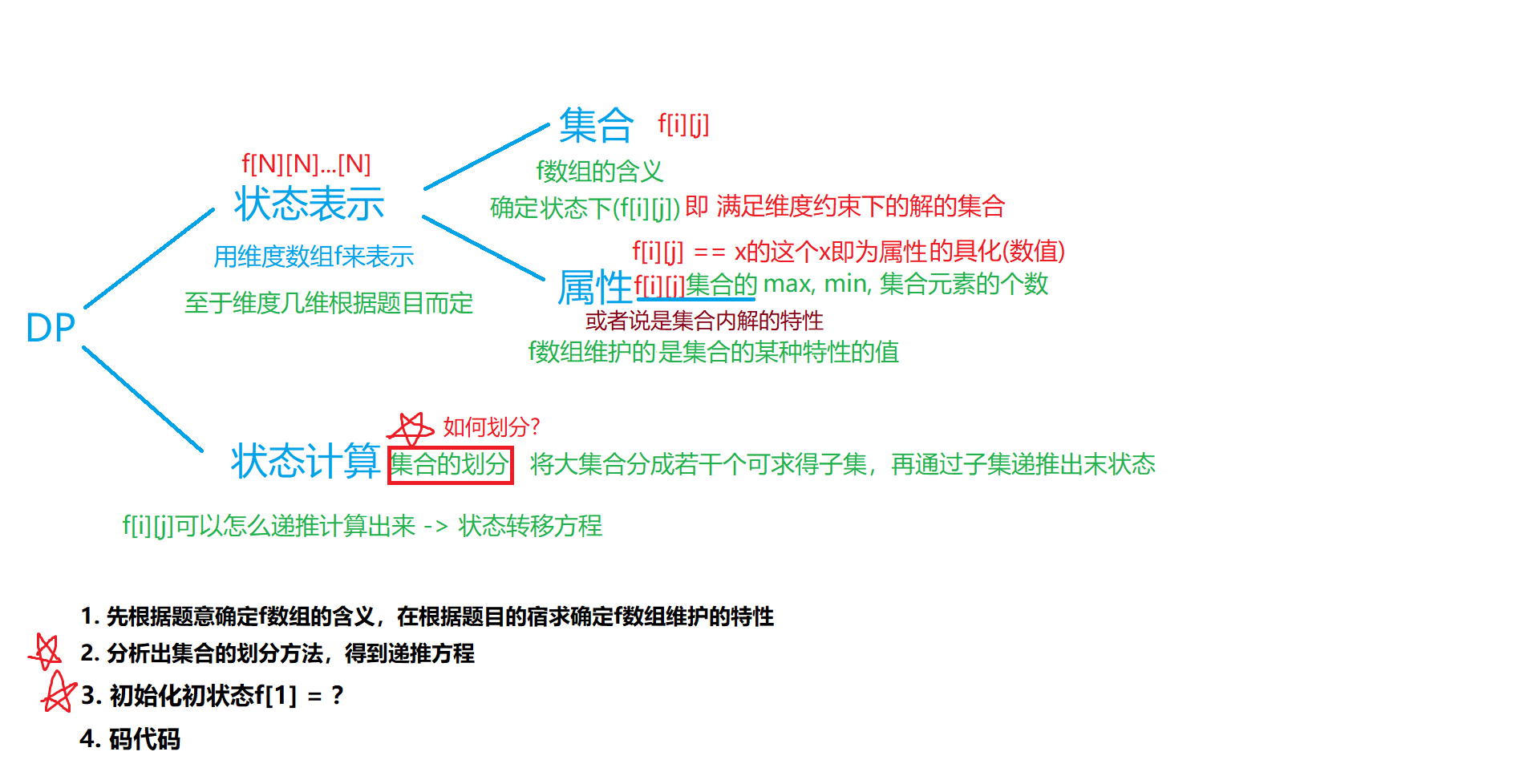
dp问题的下标
- 若状态转移方程中有f[i - 1]这种状态, 下标(状态转移那部分代码)尽量从1开始
- 否则就最好从0开始
dp问题的时间复杂度
状态数量(n^几个约束维度) * 转移状态的时间复杂(状态转移代码的时间复杂度)
dp的集合划分依据 -> 寻找最后一个不同操作
eg. 加不加这个背包, 数字三角形最后一步是由左边还是右边走过来的呀(根据操作的不同来对集合进行划分)
使得划分之后的小集合可以递推求出当前集合, 且最小集合已知

记忆化搜索
1 | Map<Integer, Integer> memo = new HashMap<Integer, Integer>(); |
java拿Map来存比较方便且省空间
- 標題: 动态规划
- 作者: sdjasj
- 撰寫于: 2022-02-19 20:32:02
- 更新于: 2022-07-19 18:49:38
- 連結: https://redefine.ohevan.com/2022/02/19/动态规划/
- 版權宣告: 本作品采用 CC BY-NC-SA 4.0 进行许可。